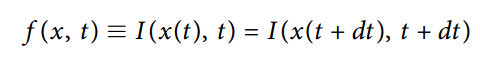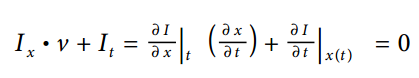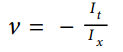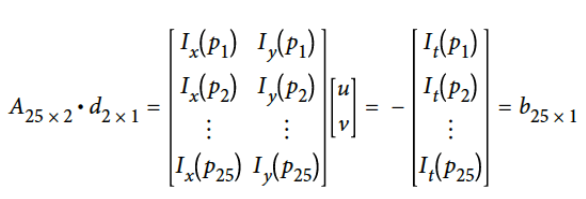|
本文截图及内容均来自learning opencv 第三版第16章 光流法主要用于寻找不同图片间的特征点对应关系。特别是应用在视频中,因为对于视频,可以合理地认为当前帧中的许多点能够在下一帧中找到。 一个理想的光流算法输出应该是图中每个像素的速度预测集合,或是表示每个像素在相邻帧间相对位置的位移向量。当对图中每个像素求解时,就是密集光流法( Lucas-Kanade算法最早在1981年提出,最初为密集光流法。因为本方法很容易应用在图片像素子集中,所以变成了一种重要的稀疏光流法。Lucas-Kanade算法只依赖于围绕关键点的小窗口推断出的局部信息。这导致了Lucas-Kanade算法不能检测到物体的快速运动到窗口外部的点。这个缺点可以通过改进的金字塔LK光流法解决。 Lucas-Kanade原理基本假设: 亮度恒定假设:目标物体像素的强度值在帧间亮度不变。对于灰度图,即对于追踪的像素点,帧间亮度不变。 时间连续:相邻帧间运动微小 空间一致性:图中临近的点属于相同的表面,具有相似的移动。
1.亮度恒定假设要求跟踪部分亮度不随时间变化:
即 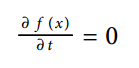 2.时间连续假定,对上式中的 I(x(t), t) 求导得:
Ix是图像的偏导数,It是图像随时间的偏导数,v是观察到的速度。对于一维空间中的光流速度等式为:
3.空间一致性: 若一个局部区域的像素运动是一致的,就可以建立邻域像素的系统方程求解中心像素的运动。如使用5x5(窗口大小)的邻域像素亮度值,计算此像素的运动,就可建立25个方程:
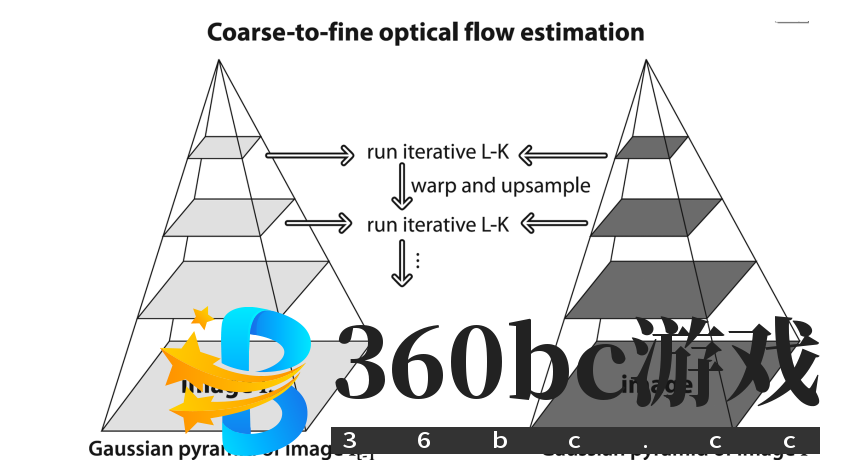
注意窗口的大小选择,窗口太大会违背空间一致性假设,太小又会追踪不到窗口外的点。 以上方法是基于小而连贯运动的假设,但是对于大多数30Hz的摄像机,大而不连贯的运动是普遍存在的。所以需要更大的窗口来追踪运动,但这又会违背空间一致性假设。因此引入图像金字塔解决。最初在较大的空间尺度追踪,再在小的空间尺度上修正。
追踪方法:在图像金字塔最高层计算光流,得到的运动结果作为下层金字塔的起始点,重复这个过程直至最底层。这样就將不满足运动假定的可能性降到最低并实现更快更长的运动追踪。这个方法就叫金字塔Lucas-Kanade光流法。 在OpenCv中的实现函数为calcOpticalFlowPyrLK。 |